Pairs of Lines

First Glance

In geometry, a line is a straight curve that extends indefinitely in both the directions. A pair of line can be related to each other in four different ways namely- intersecting lines, parallel lines, perpendicular lines and lastly but not the least skew lines.

Intersecting Lines: Two different straight lines on the same plane in two different directions meeting at only one given point are called Intersecting Lines. The meeting point is called “Point of Intersection.” In the above figure, Line GH intersects line KL at point P.

Parallel Lines: Two different straight lines on the same plane in two different directions who never meet at any point, no matter how much they are extended are called parallel lines. In the above figure, Line MN is parallel to Line OP.

Perpendicular Lines: Two different straight lines on the same plane in two different directions who meet each other at only right angles are called Perpendicular Lines. In the above figure, Line AB is perpendicular to Line EF and APF = 90°

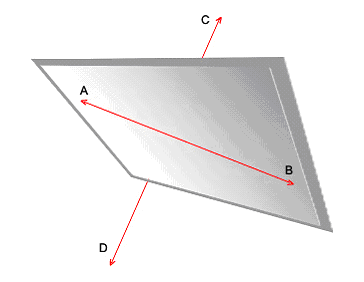
Skew Lines: Two different straight lines not lying on the same plane in two different directions, who do not meet each other no matter how much they are extended. In the above figure, Line AB is located on a different plane and Line CD is located on a different plane.

Details:

There are several pairs of intersecting line segments – for example, line segment DC and line segment FC share one point in common, point C, so they are intersecting line segments.

Practically, in geometry it is seen that the lines often come in pairs. There are four different types of line pairs: lines that intersect, lines that are perpendicular, lines that are parallel, and lines that are skew. Now the question arises why do we need to focus on these aspects? Actually, these initial concepts are important for understanding and solving various geometrical problems. A picture of a box (a cube) given above is used to explore and understand each of these line pairs, which are the basics of geometry.

Intersecting Lines: Intersecting lines are lines that meet at a certain point and have just one point in common. When two lines intersect, they form angles at the point of intersection. In the above figure of the box there are several pairs of intersecting line segments for example – line segment HE intersects line segment FE at point E, hence the line segments HE and FE are Intersecting Lines.

Perpendicular Lines: Perpendicular lines intersect at one point and form a 90° angle. The x and y axes on the coordinate plane are the perfect examples of perpendicular lines. In the given box above has many perpendicular line segments for example AH and EH are perpendicular to each other. Actually, in a cube all angles formed by intersecting lines are 90°.

Parallel lines: Parallel lines are lines that never intersect no matter how much are they extended. The distance between the two lines is fixed and the two lines are going in the same direction. In the given box above, Line segments DC and EF are parallel.

Skew lines: Skew lines are two lines that do not intersect but are neither parallel. Skew lines unlike parallel lines are not in the same plane. To be skew lines it must not intersect and at the same time must not be in the same plane. In the given box above observe edge DC on the left front side of the box, moving up and down, and edge HG at the bottom back, moving left to right. These line segments neither intersect each other nor are neither in the same plane. Thus, these line segments are skew lines.

Examples

Referring to the above figure, we can conclude:

• AB is perpendicular to CL and CIB is 90°
• KE intersects IB at point J
• GH is parallel to AB
• KD is perpendicular to MH and KLH is 90°
• IL intersects JM at point K
• EF intersects GL at point M, intersects IL at point K and IB at point J

Test your knowledge – try our Pairs of Lines Test.