
Circle Properties
The Basics:
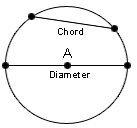
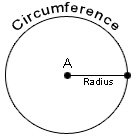
A circle is a plane figure bounded by one curved line where all of its point is at a constant distance from a fixed point in the plane, which is termed as the center of the circle. The constant distance of every point on the circle from its centre is called the radius of the circle. As we move ahead, it’s important for the learners to get acquainted with the basic terms related to a circle.
Circle: A circle is a set of those points in a plane, which are at a constant distance from a fixed point in the plane.
Radius: The distance from the center of a circle to any given point on the circle is known as the radius of a circle
Diameter: Any straight line drawn through the centre and ending at both ways by the circumference is called diameter. Diameter is just the double of radius.
Circumference: The distance around a circle, which is the bounding line is called the circumference.
Chord: A straight line joining any two points on the circumference of a circle is called a chord.
Arc: Any portion of the circumference of a circle is referred as an arc
In Detail:
As you gaze around, you must have come across different geometrical figures like square, rectangle and others in some form or the other. Surely, a circle is also no exception. The most common sight of a circle would be the wheel. Have you ever noticed the base of a flower-vase, bucket or a coffee -mug? The bases of all these objects are circular.
A point lying inside a circle is called an interior point of the circle whereas a point lying outside a circle is termed as an exterior point of the circle. Similarly, the set of interior points of a circle is called the interior of the circle whereas the set of all exterior points of a circle is called the exterior of the circle.
Remember, all the diameters of a circle are equal. Similarly all radii (plural of radius is radii) of a circle are equal, since all the points on the circumference are equidistant from the center. In the given picture where the centre is O and the AB is the diameter of a circle and OA and OB are radii.
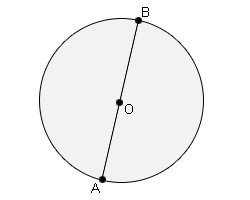
| It is important to understand that since OA = OB |
| OA+OB= AB |
| AB = 2 x OA |
| Or, AB = 2 x OB |
Picture:
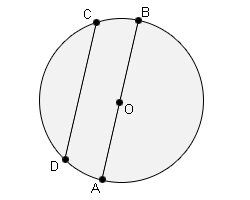
A straight line connecting any two points on the circumference of a circle is called a chord. In this context, it must be remembered that if a chord passes through the centre, it becomes diameter. Therefore, a diameter is also a chord, which passes through the centre.
In the above given picture AB and CD are the chords of the circle. Any diameter divides a circle into two equal parts and each part is known as semi-circle. In the given picture diameter AB divides the circle into two equal halves.
Congruency of a circle: Two circles can be called congruent if and only if one of them can be superposed on the other to cover it completely. In other words, if the radii (plural of radius) of two circles are of same measurement, then the two circles are congruent.
The degree measure of a circle is 360 degree. An arc is the portion of the circumference of a circle. Arcs are measured in degrees similar to angles and can be classified into major arc, minor arc, and semi- circles. The larger of the two arcs is called the major arc, which measures between 180 and 360 degrees and the smaller one is called the minor arc which is between 0 and 180 degrees. The measure of a semi-circle is 180 degree.
Different Types of circles:
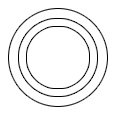
Concentric circles: Circles having the same centre but different radii are known as concentric circles.
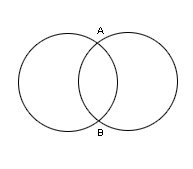
Intersecting Circles: When two circles cut each other at two different points, they are called intersecting circles.
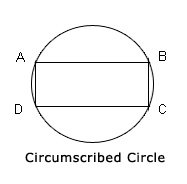
Circumscribed Circle: A rectilinear figure is said to be inscribed in a circle when all its angular points lie on the circumference of a circle then the circle is referred to be circumscribed in respect to that figure
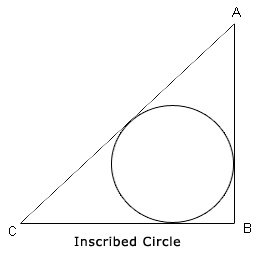
Inscribed Circle: A rectilinear figure is referred to be circumscribed in a circle when all its sides are tangent to the circle. Then the circle is referred to be inscribed in respect to that figure.
In the previous chapter of angles, you have come across a protractor used for measuring angles. As you touch the circle portion of geometry, you will come across another geometrical tool – compass used for the construction of a circle apart from its other uses.
If you feel you’re ready, try the circle test.



