
Basics of Geometry
The world comprises of many things. Some are tangible while others are intangible, which can only be imagined. It is here the visualization aspect of geometry is reckoned. Thinking analytically, geometry originated as a practical science, concerned with surveying, measurements, areas and volumes. The practical significance of geometry can be understood when you see the world around you – from the lofty manmade bridges to hitting the ball in a billiards game. The importance of geometry in this modern era cannot be undermined. It’s interesting to know that the mighty pillar of geometry rests on the simple but important ideas like point, line, plane, and space respectively.
- Point: A small dot made by a pencil or a plane of paper gives an idea of point. It is dimensionless, so it has no length breadth or width. A point has a position and its location can be determined. In the given figure, the letter P indicates a point.

- Line: A set of points make a line, which has only one dimension i.e. length. There can be a number of points lying in a straight line. In short, a line has arrowheads on both sides showing that a line extends on both sides indefinitely. Points on the same line are referred as “collinear points.†Minimum of two points are needed to form a line. In this case AB is a line.

Notice how to write the symbol for this line. The arrowheads on line AB show us that the line extends endlessly in both directions.
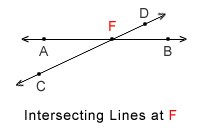
Intersecting line: When two lines meet at a point, they are called “intersecting lines.” In the above diagram both the lines CD and AB meet at point F.
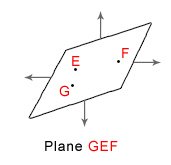
- Plane:  A solid has a surface, which can be flat or curved. Flat surface is known as plane surface. The surface of a table is an example of a plane. A plane is commonly named by taking three or more points on it, which are not on the same line.
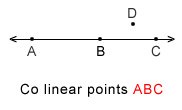
Co-linear Points: Three or more points in a plane are said to be co-linear if they all lie on the same line, this line is the “line of co-linearity.†In the above diagram Points A B and C are co-linear but Point D in non co-linear.
Concurrent Lines: Three or more lines in a plane are concurrent if all of them pass through the same point. The point of intersection is called the point of concurrence. In the above diagram AB, CD and EF are concurrent lines where G is the point of concurrence.

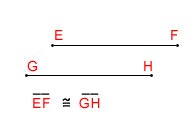
- Line segment: Line segment is a portion of line or straight path, which has specific length and specific endpoints. A line segment is completely known if its end-points are known. Sometimes we use the word “segment†for a line segment.  Two line segments of equal length are termed congruent segments. The symbol
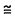 Â indicates that EF is congruent to GH.
 indicates that EF is congruent to GH.
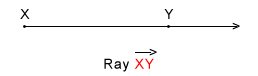
- Ray: A ray is a part of a line that extends indefinitely in one direction. A ray has only one end point. The symbol of a ray is

- Angle: An angle is formed by two rays with the same initial point. The common endpoint is called the vertex of the angle and the rays forming the angle are called the arms. In the above diagram Point C is the vertex and the arms of the angle are CE and CD. The symbol of an angle is
 Â Â . In order to define an angle you have to always keep the point depicting the vertex at the middle, Thus, in this case you can define this angle as
  . In order to define an angle you have to always keep the point depicting the vertex at the middle, Thus, in this case you can define this angle as 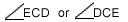

Test your knowledge – try this Geometry Test.



