
Division Tips and Tricks
Division is easy to learn if you know how to add and multiply WELL.
Tip #1
Let’s look at a division problem to learn the key terms and how to solve them. The problem below labels the parts of a division problem.
_3_ <--- quotient (The Answer)
(What's dividing) divisor---> 2 )6 <--- dividend (What's being divided up)
Here is the same problem in a different form, 6 ÷ 2 = 3
In words, we would say; six, divided by two, equals three.
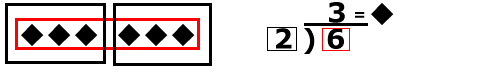
Another way to look at it: you have 6 things to go into 2 boxes. How many will be in each box?
In the space provided, label the parts of the following division problem and put it into a new form.
_4_ <--- __________
________---> 3 )12 <--- ____________
_______÷_______= ______
In the space below, write the problem in words or as it would be said aloud.
Let's look at the same problem without an answer.
___ <--- quotient ( The Answer)
(What's dividing) divisor---> 3)12 <--- dividend (What's being divided up)
TO SOLVE THIS DIVISION PROBLEM WE ASK:
"3, TIMES WHAT, EQUALS 12?" -OR- "WHAT TIMES 3 EQUALS 12?"
This converts the division into 3 × ? = 12. Which we can easily solve with a 4.
Let's practice with another division problem, fill in the blanks:
To solve the problem 18 ÷ 6 = ___
First, we __________ the division to the ______________problem 6 × _ = 18 As a multiplication champion, you'll know that the answer is ____.
In summary, the following are all the same problems in different formats.
18 ÷ 6 = 3 _3_ 6
6 )18 × 3
18
In the spaces below, convert the following divisions to multiplications and solve.
___ ___
5 )15 ×____
___ ___
4 )12 ×____
___ ____
6 )18 ×____
Now, go here for division worksheets you can use with converting divisions to multiplications (no remainders).
Tip #2
Sometimes with division problems the answer will result in an what's called a remainder. So, let's learn to solve a problem using long division and find out what a remainder is.
Here is the problem:
___ 3
3 )16 ×____
16
To solve we ask, "what times 3, equals 16?" Since 3 × 5 = 15 and 3 × 6 = 18 the closest we can get is 15 without going over the dividend number. Let's write that in and subtract 16 - 15 = 1 as shown below.
__5_r1 The "r" stands for remainder
3 )16
-15
1
A remainder occurs whenever one number is NOT totally divisible by another number. The remainder is really a fraction. In the above problem, we could write the result as 5 and 1/3
Solve the following problems using long division and multiplication, show the remainders as fractions if possible:
___ or 4
4 )27 ×____
27
___ or 2
2 )25 ×?
25
As we progress along in division, we might run into problems like the following:
___ or 3
3 )125 ×?
125
Step 1:
Work the problem from the 100s, to the 10s then to the 1s -or- from left to right.
___ or 3
3 )125 ×?
125
Start by looking at the number in the 100s column (1) and ask yourself, "3 times what equals 1? or, "how many 3s in 1?" (the 1 comes from the 1 in 125). Since 1 can't be divided by 3 easily, skip it and look at the number to the right of it in the 10s place or the 2.
Step #2
___ or 3
3 )125 ×?
125
Now put the 1 and 2 together for a 12 and ask,"what times 3 equals 12?" or, "how many 3s in 12?"
The 12 comes from the 12 in 125.
HELLO!
4 × 3 = 12. We've solved part of the problem...YES!
Step 3:
Now, here's the twist, add 0s to the 4 and to the 12 and make them a 40 and a 120. So now your multiplication should be 3 × 40 = 120
__40_ or 3
3 )125 ×40-120 120
5
Place the 40 OVER the problem in
the quotient area as shown.
Now, place the 120 UNDER the 125 as shown above and below.
__40_ or 3
3 )125 ×40
-120 120
5
Step 4:
Subtract 120 from 125 and you should get 5.
Now ask, "what time 3 equals 5?" or "how many 3s in 5?"
If you answered 1, great!
Now put a 1 above the 40 in the quotient area and subtract 3 from 5 as shown below.
1
__40_ or 3
3 )125 ×1-120 3
5
-3
2
Now add the quotients together and bring the 2 up from the bottom of the problem and you should have the complete answer...41 r2.
Tip #3
How to solve even tougher problems.
To solve tougher division problems, break dividends into 100s 10s and 1s then estimate to find solutions. In a problem like:
___ or 8
8 )983 ×?
983
Working from left to right we start to estimate with 100's and ask, "8 times what equals 900" or "what times 8 equals 900?"
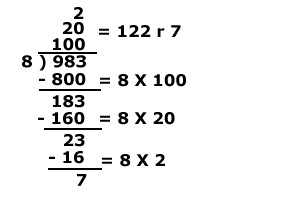
Then, in estimating 100s we find that 100 × 8 = 800 and that 200 × 8 = 1600... but we can't subtract 1600 from 983. So, lets start with 100 × 8 = 800 and subtract 800 from 983.
_100_ or 8
8 )983 ×100-800 800
183
Now we ask, "how many 8s in 183?"
We know that 8 × 2 = 16 so we estimate by 10s and find that 8 × 20 = 160. Wow, that close, let's subtract that amount next.
20
_100_ or 8
8 )983 ×20-800 160
183
-160
23
Now, all we have to find out is how many 8s in 23. Sheesh, 8 × 2 = 16 and that's close. Let's subtract that amount next and finish this problem.
2
20
_100_ or 8
8 )983 ×2
-800 16
183
-16023
-16
7
Then add the numbers in the quotient and post the remainder with it and you get 122 r7.
Here's another look at that with an even tougher problem.
2,356 ÷ 18           18s
estimate how many 100s of 18s in 2,300
then, how many 10s of 18s
then, how many ones of 18__
18 )2356
-1800 100 × 18
556
-180 10 × 18
375
-180 10 × 18
195
-180 +10 × 18
16 130 r 16



