
Subtraction Tips and Tricks
Your learner should know how to count, print numbers, add and a little about place value before trying to subtract.
From my experience, a learner’s subtraction problems arise from their lack of addition savvy. Therefore, my first suggestion for aspiring Subtraction Champions is to “overlearn” addition.
Overlearning is a process where a learner has mastered ALL the basic addition facts through memorization.
In other words, for your learner to become a Subtraction Champion, don’t ignore the importance of addition fundamentals. If you feel your learner could use more help with addition, please see Addition Tips and Trickslocated in the index section of this site and follow the recommendations.
So, if you feel that your learner is an Addition Champion and is ready to dive into subtraction, here are my Tips and Tricks:
Tip #1
The first trick is to treat subtraction like additions missing an addend. For example, take a problem like 7 – 4. Use the 7 as the answer and the 4 as an addend like this…”what plus 4 equals 7″ OR __+ 4 = 7. If you’re an addition champion you’ll know right away that the answer is 3.
Try turning the following subtractions into additions:
Example:
4 – 3 = 1 –> 1 + 3 = 4
6 – 2 = Say, “what plus 2 equals 6?” _____+_____ = ______
5 – 3 = Say, “what plus 3 equals 5?” _____+_____ = ______
7 – 2 = Say, “what plus 2 equals 7?” _____+______= ______
I’m working on an activity worksheet here for you to practice this exercise.
NOTE: To help your learner memorize these problems, try reading the equations, then cover them, then recite them, then check to make sure the learner recited it correctly…this is called R.C.R.C. -or- R ead, C over, R ecite, C heck. After you have R.C.R.C.’d the equation, come back to it later to make sure your learner remembers it…repeat the R.C.R.C. often (each learner is different…some will get it in several tries, others may take ???) with each problem.
Tip #2
In subtraction, two rules apply. One rule is that a number subtracted by the same number is always zero (0). Example: 2 – 2 = 0. Memorize the following equations to speed your learner’s ability to solve problems:
- 1-1=0
- 2-2=0
- 3-3=0
- 4-4=0
- 5-5=0
- 6-6=0
- 7-7=0
- 8-8=0
- 9-9=0
When your learner has those memorized, it will be easier to figure out what 7-6 is because it will be one more than 7-7 (so, 7-6=1). Likewise, it’s also easier to figure out what 8-7 is since it’s one more than 7-7 (so, 8-7=1….see?)
Tip#3
The second rule of subtraction is, zero subtracted from any number equals any number. Example: 5 – 0 = 5.
So:
- 9 – 0 = 9
- 8 – 0 = 8
- 7 – 0 = 7
- 6 – 0 = 6
- 5 – 0 = 5
- 4 – 0 = 4
- 3 – 0 = 3
- 2 – 0 = 2
- 1 – 0 = 1
Tip#4
Memorize the essential subtraction problems. Here is a list of subtractions that are essential to learn:
|
|
| ||
|
|
|
|
|
O.K., drill (memorize the above problems) and any other subtraction problems will be easy.
The next area of subtraction that causes problem is subtracting through a multiple of ten. A number with a multiple of ten is, for example, 10, 20, 30, 40,…100. 120, 240, 580, etc,… For some reason this has a tendency to mix learners up. So, here are some more problems that should help. Here I think it’s important to point out a TRICK with the number 9.
TRICK: When subtracting a nine the answer will always be one “MORE” than the last digit of the first number of the subtraction. For example, in the problem 11-9=2 the answer 2 is one “MORE” than the last digit of the 11 or “1” this means the answer is 2. See what I mean? This works for problems like 27-9=18 the last digit of 27 or “7” is one more than the last digit of the answer 18. Cool!
Tip #5
Learning to borrow or rename is another way to help subtract through a multiple of 10. We borrow or rename whenever the upper number in a subtraction is of less value than the lower number.
For example, in the problem below we’re subtracting 25 from 40. In the ones column (0 – 5) we can’t subtract because we can’t subtract 5 from 0 or nothing. So we borrow 1 from the 4 to the left of the 0. Cross out the 4 as shown and write a 3 above the 4. Write the 1 to left (or tens column) of the 0 making it a 10. Now subtract 5 from the 10. Below the
line, write a 5 in the ones column. Now subtract 3 – 2 = 1 and write the 1 to the left of the 5. The answer is 15.

Let’s take a look at another problem below.
Here we are subtracting 134 – 78.

In the ones column 4 – 8, we have to borrow 1 from the left (3). So do that by crossing out the 3 and writing a 1 to the left of the 4 as shown. Now subtract 8 from 14 for 6. Then subtract 70 from 120 for 50. Then, add the 50 + 6 together for 56.
Is this making any sense yet?
If not keep going. If it is try these practice problems.
More on Borrowing or Renaming
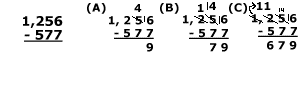
In the example above, we subtract 577 from 1,256. We must borrow three times as shown.
- First, cross out the 5 (in 1,256) and put a 4 above it as shown in (A). Then, give a 1 to the 6 to make it 16 – 7 = 9.
- Second, cross out the 2 (in 1,256) put a 1 above it and give 1 to the 4 making it 14 – 7 [in 5(7)7] = 7 as shown in (B).
- Third, Cross out the 1 (in 1,256) and give 1 to the 1 making it 11 – 5 = 6 as shown in (C).
- And finally, the answer is 679
To check and see if you’ve subtracted a problem correctly, don’t forget to add the answer you got to the number above it and the sum should be the top number.
For example, in the problem 7 – 3 = 4 we would add the 4 to the 3 and get 7. Get it?



