
Squares / Square Roots
Basics:
p is the symbol of square root and its origin actually dates back to hundreds of years ago. The symbol is also called the radical.

Suppose you have to calculate the number of little squares in the large square, the first thing that will come to your mind is to count the number of boxes, which are of equal sizes. It may be a way but it may often lead to confusion, as all the boxes look similar. However, there is an easier way to know the number of boxes if you know the size of the each side of bigger square.
Suppose the size of each side is 6 cms then you can easily find out the number of squares by just multiplying side with side. In this case, the number of small boxes will be 6 x 6 = 36 boxes.
If the inverse information is provided and asked to find the size of sides and if it is said that there are 36 equal size squares in a bigger square and you need to find the size of the side, it is possible too only with the reverse operation. It will be done by √36 = 6. This helps to find out the sides of a square if the area is provided.
More Detail:
The square can be used to model a number that is raised to the power by 2 and that is why whenever a number is raised to the second power it is called “squaring the numberâ€. Moreover, any perfect square is actually squares of whole numbers. You should be very much aware of the squares and square roots of few numbers most commonly used.
Some squares are as follows:Â Â Â Â Â
12 Â = 1
22 Â = 4
32 Â = 9
42 Â = 16
52 Â = 25
Some square roots are as follows:
√36 = 6
√49 = 7
√64 = 8
√81 = 9
√100 = 10
Pre-Algebra and Algebra may have got all of us in touch with squares and square roots but it is equally important in Geometry. Squaring a number is just multiplying the number with itself while finding the square root is just the inverse operation. There are different models to learn the concept of squares and square roots.
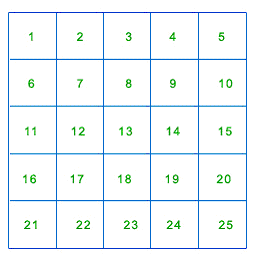
The figure represents a square with sides 5cm each. The square is divided into boxes having sides 1cm each. Therefore, the area of the square must be the summation of all the areas of the small squares inside the box. Thus, the number of boxes can be easily calculated if you know the square of 5. Thus, square of 5 is 5 × 5 = 25cm2 and if the area of square is given 25cm2 then the sides of the square will be √25 = 5 cm.
Examples
Find the value of x in each of the following:
√x = 5,
Thus, x = 52 = 25
x2 = 49
Thus, x = √49 = 7
√25 = x
Thus, x = 5
Test your knowledge – try our Squares and Square Roots Test.



