
Prisms: Properties and Types
The Basics
In geometry, the polyhedron with two parallel polygonal bases is called prism. In a prism the cross sections which are parallel to the base resemble each other. There is also a definite formula to calculate the area and volume of prisms. The unit for representing the area is square units and the volume is cubic units. There are different kinds of prisms as well. Some of them are:
Rectangular prism

A rectangular prism is a 3-dimensional object, which has as many as six faces. It is a solid material and all the faces are rectangular. One more reason because of which it is regarded as a prism is that it has the same cross section along a length.
Hexagonal prism

A hexagon has six sides and a hexagonal prism has six sides and two bases. It is mostly considered as a space-filling polyhedron. Moreover, the regular right hexagonal prism has a definite formula to calculate the surface area and volume.
Triangular prism

Two triangular bases and three rectangular sides make a triangular prism. It falls in the category of a pentahedron.
More Details
Hexagonal prism
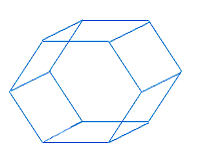
The polyhedron, which has two congruent parallel polygons as its bases, is called a prism. The other faces that the prism has are parallelograms as well. The shape of the base contributes in naming it as prism. The name, hexagonal prism is given to describe the particular shape of its bases. The bases of a hexagonal prism are typically hexagonal. The formulas used to calculate the area and volume of a hexagonal prism are as follows:
Area = 3(2 + √3) a2, where a = edge length
Volume = 3/2√3a3
Rectangular prism

The above figure is a rectangular prism in its unfolded form. Think it to be an open paper box. You need to observe it carefully about how you can get a rectangular prism from the above figure. If you still can’t get a clue, the next figures will make it clear for you.
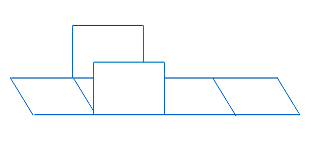
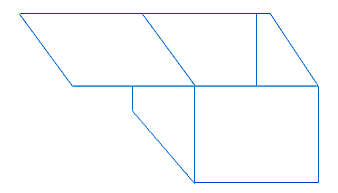
Now, you can understand that once you fold it in an appropriate manner you will get a rectangular prism. The presence of 6 congruent faces in the rectangular prism qualifies it as a “regular hexahedron†as “Hexa†means six in Greek.
The definite formulas to calculate the area and volume of a rectangular prism are:
Area = 2(wh + lw + lh), where l = length, w = width, h = height.
Volume = lwh
Triangular prism
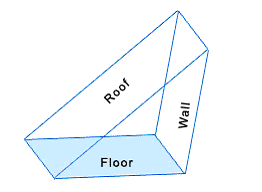
The triangular prism also has some unique features. This pentahedron has 3 rectangular faces and two triangular faces. The formula for calcuating the area and voume of a triangular prism is
Area of prism = 2 x Area of base + Perimeter of base x H
Volume = Area of the base x height
Examples

Question:
Find the volume of a rectangular prism with base 5 inches by 3 inches and height 7 inches?
Answer:
Volume of rectangular prism = lbh
or, V = (5 x 3) 7
or, V = 15 x 7
or, V = 105 inch3
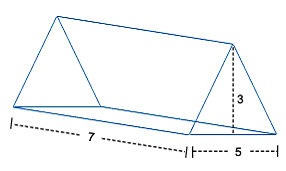
Question:
Find the volume of a triangular prism with sides 7 inches, 3 inches and height 5 inches?
Answer:
Volume of the prism = Area of triangular base x height
or, V = ½ x 5 x 3
or, V = 7.5 inch2 x 7
or, V = 52.5 inch3
Test your knowledge – try our Prisms Test.



