
Ratios and Proportions
Ratio:
When we compare two quantities, which are of the same kind in the form of a division, it is said to have formed a ratio of the two quantities. The symbol : (colon) is used to represent a ratio. For instance, 2:4 is a ratio. Ratios are also expressed in words and during that time the word ‘to’ is used. Must be wondering, how it comes. Here it is:

As a fraction, you can express the above as ![]()
If you use the word “to,†you can express the above relationship as 3 to 2
Using a colon, you can say 3:2
As mentioned earlier a ratio is all about comparison between two things. The above diagram reveals some figures in green and orange. If you consider ratio of green leaves to orange flowers then the ratio will be 3:2 and in words it will be said the ratio of leaves to flowers is three to two. Moreover, ratios are also revealed in form of a fraction as the above ratio can be expressed as 3/2 where the first term becomes the numerator and the second term is invariably the denominator.
There is also a definite name for the first term and the second term. For instance, 3:4 is the ratio. In this ratio, 3 is the first term and can also be called as antecedent and 4, which is the second term can also be called consequent. Another important thing that needs to be known while expressing ratio is that it is always expressed in simplest forms.
Proportion:
Proportion is an equality of two ratios. When two ratios are divided or multiplied with an identical nonzero number it provides us an equal ratio. Moreover, when two ratios are equal even the cross products are equal.

However, how will you understand that the two ratios are equal. It is a simple process, that involves dividing the ratios. If both the division give the same result then they are equal. For instance there are two proportions:
a:b and c:d and a:b = c:d, then it is a proportion. ‘a’ and ‘d’ are situated at the two ends so they are called Extreme Terms or Extremes and ‘b’ and ‘c’ situated at the middle are called the Middle Terms or Mean.
Moreover, if the middle term is repeated then each of the middle term is called mean proportional. For instance, if the proportion is a:b = b:c then ‘b’ is called mean proportional.
More Detail:

If the number of leaves and number of flowers is represented in terms of ratio then it will be 3:6 or 3/6, according to the form you want to represent. However, it should always be expressed in simplest form. As a result, if we divide both the terms of the ratio by 3 then the ratio becomes 1:2. But, after dividing the ratio has not changed all over. The 3:6 ratio is only expressed in its simplest form 1:2 and as a matter of fact they are equal ratios. Numerous ratios can be equal to them. For instance, ratios like 4:12, to100:300 are equal ratios as you can divide these ratios and get the same quotient. However, ratios like 1:2 to 3:7 are not equal as you divide the ratios, you won’t get the same quotient.
A proportion is simply a statement that two ratios are equal. It can be written in two ways: as two equal fractions a/b = c/d or using a colon, a:b = c:d. The following proportion is read as “ten is to twenty as two is to four.”
![]()
In problems involving proportions, we can use cross products to test whether two ratios are equal and form a proportion. To find the cross products of a proportion, we multiply the outer terms, called the extremes, and the middle terms, called the means.
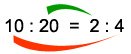
A proportion which states that two ratios are equal also have different forms of expression as it can be expressed like a:b = c:d or a/b = c/d. You can read proportion in a certain way as well. For instance a proportion of:
![]()
can be read as “ten is to twenty as two is to four.” The cross products are also a great way to check a proportion. For instance, taking the same proportion if we cross multiply two fractions, then both of them give the result 40 and states that they are equal ratio.
The cross products also serve another purpose apart from clarifying the equality of the ratio. For instance if you take the following problem:
The city authorities built a 5ft high model of a building and showed it to the citizens. The citizens loved the model and the city authorities built a building 50 ft high. The following year keeping the same ratio the city authorities built a model 8ft high, then what would be the height of the building in reality?
The first step to solve such a problem is to assume the missing quantity as a. Here the height of the building to be built should be considered a . Now you can express the relationship as:
5 : 50 = 8 : a (since, a 5ft high model is used to build a 50ft high building, an 8ft high model should be used to build “a†ft high building)
Thus, by cross-multiplying we get:
50 x 8 = 5 a (multiplying means and extremes)
or, 400 = 5a
or, 80 = a
Thus, the height of the actual building whose model is 8 ft high should be 80 ft.
Examples
Question:
Give two equal ratios for 3:6
Answer:
3:6 = 9:18 (Multiplying each ratio by 3)
3:6 = 12:24 (Multiplying each ratio by 4)
Question:
Change the form of the following ratios 3:6, 2 to 7, 4/12
Answer:
3:6 can also be represented as 3 to 6 or 3/6
2 to 7 can also be represented as 2:7 or 2/7
4/12 can also be represented as 4:12 or 4 to 12
Question:
Write the following ratios in its simplest form 36:45, 48:12, 225:30 and 13:39
Answer:
36:45 = 36/45 (Dividing both the terms by 9) we get 4:5
48:12 = 48 / 12 (Dividing both the terms by 12) we get 4:1
225:30 = 225 / 30 (Dividing both the terms by 12) we get 15: 2
d) 13:39 = 13 / 39 (Dividing both the terms by 12) we get 1:3
Question:
Find out whether the following equation is in proportion:
![]()
Answer:
Using cross multiplication rule, we can verify 36 x 3 = 18 x 6 or 108 = 108, which means the equations are in proportion.
Question:
Find the value of “a†in this proportion:
![]()
Answer:
By Cross Multiplication, we get:
5 x a = 15 x 3
or, 5a = 45
or, a = 45 / 5
or, a = 9
Test your knowledge – try our Ratios and Proportions Test.



